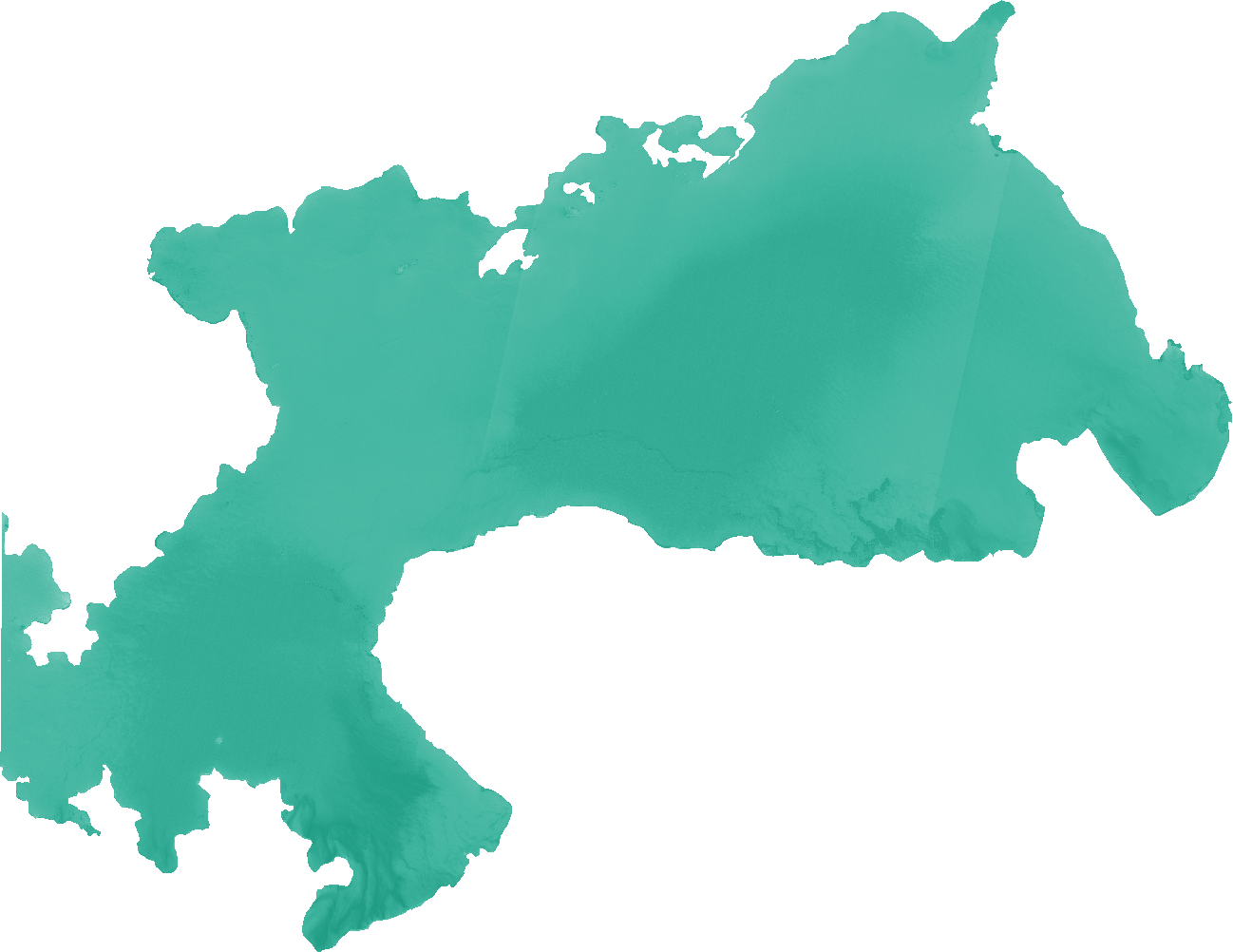
The Normalized Difference Water Index algorithm was developed by Gao (19964) being a measure of liquid water molecules in vegetation canopies that interacted with the incoming solar radiation. NDWI is sensitive to changes in liquid water content of vegetation canopies. It is less sensitive to atmospheric effects than NDVI. NDWI does not remove completely the background soil reflectance effects therefore it should be considered as an independent vegetation index. It is complementary to not a substitute for NDVI. The NDWI results from the following equation: NDWI = (IR_factor * near_IR - mir_factor * middle_IR) / (IR_factor * near_IR + mir_factor * middle_IR)

The Weighted Difference Vegetation Index algorithm was introduced by Clevers (1988). This has a relationship to PVI similar to the relationship IPVI has to NDVI. WDVI is a mathematically simpler version of PVI but it has an unrestricted range.Like PVI WDVI is very sensitive to atmospheric variations (Qi et al. 1994). The WDVI results from the following equation: WDVI = (IR_factor * near_IR - g * red_factor * red) where: g is the slope of the soil line.

The Normalized Difference Water Index algorithm was developed by Gao (19964) being a measure of liquid water molecules in vegetation canopies that interacted with the incoming solar radiation. NDWI is sensitive to changes in liquid water content of vegetation canopies. It is less sensitive to atmospheric effects than NDVI. NDWI does not remove completely the background soil reflectance effects therefore it should be considered as an independent vegetation index. It is complementary to not a substitute for NDVI. The NDWI results from the following equation: NDWI = (IR_factor * near_IR - mir_factor * middle_IR) / (IR_factor * near_IR + mir_factor * middle_IR)

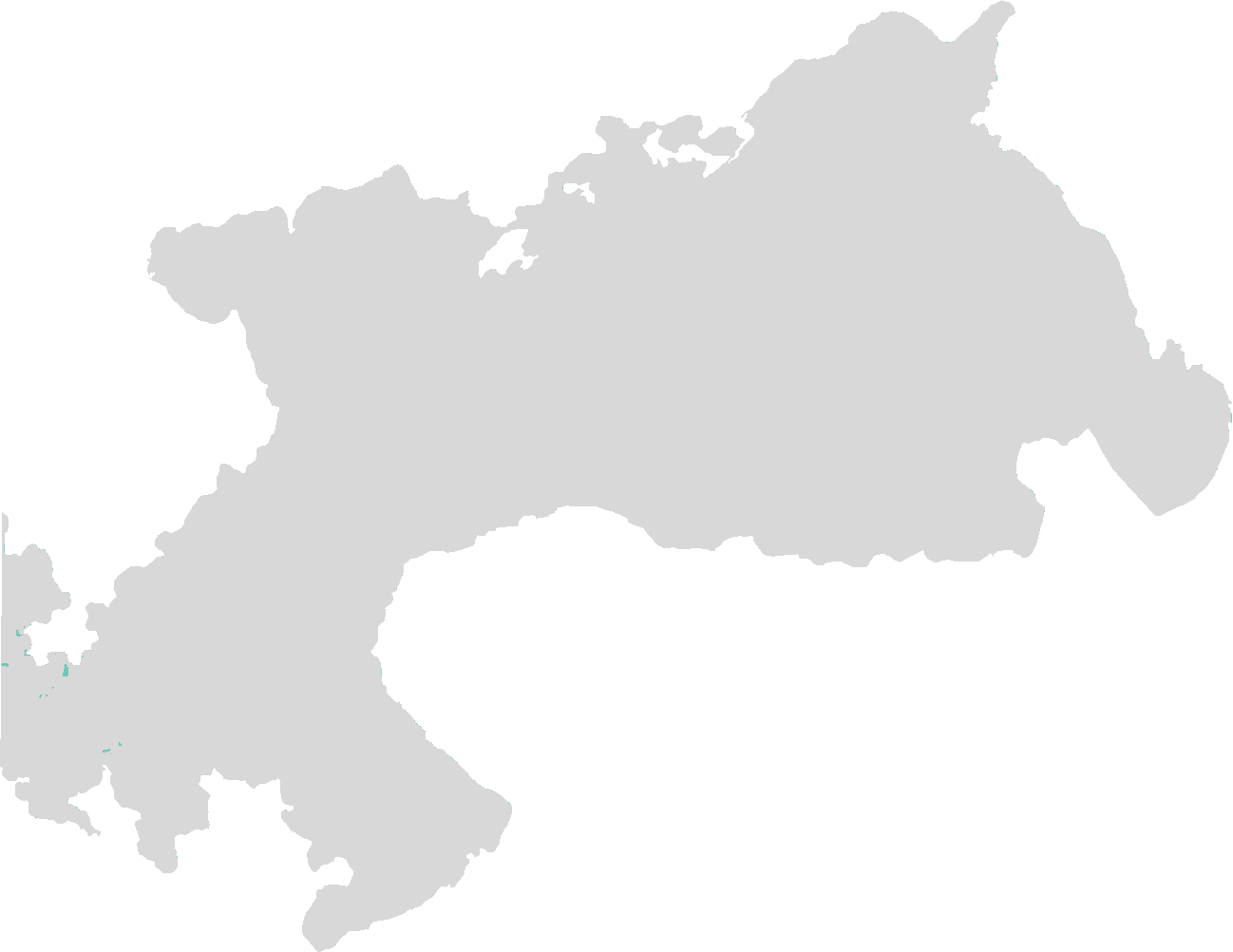
The Weighted Difference Vegetation Index algorithm was introduced by Clevers (1988). This has a relationship to PVI similar to the relationship IPVI has to NDVI. WDVI is a mathematically simpler version of PVI but it has an unrestricted range.Like PVI WDVI is very sensitive to atmospheric variations (Qi et al. 1994). The WDVI results from the following equation: WDVI = (IR_factor * near_IR - g * red_factor * red) where: g is the slope of the soil line.

The Weighted Difference Vegetation Index algorithm was introduced by Clevers (1988). This has a relationship to PVI similar to the relationship IPVI has to NDVI. WDVI is a mathematically simpler version of PVI but it has an unrestricted range.Like PVI WDVI is very sensitive to atmospheric variations (Qi et al. 1994). The WDVI results from the following equation: WDVI = (IR_factor * near_IR - g * red_factor * red) where: g is the slope of the soil line.

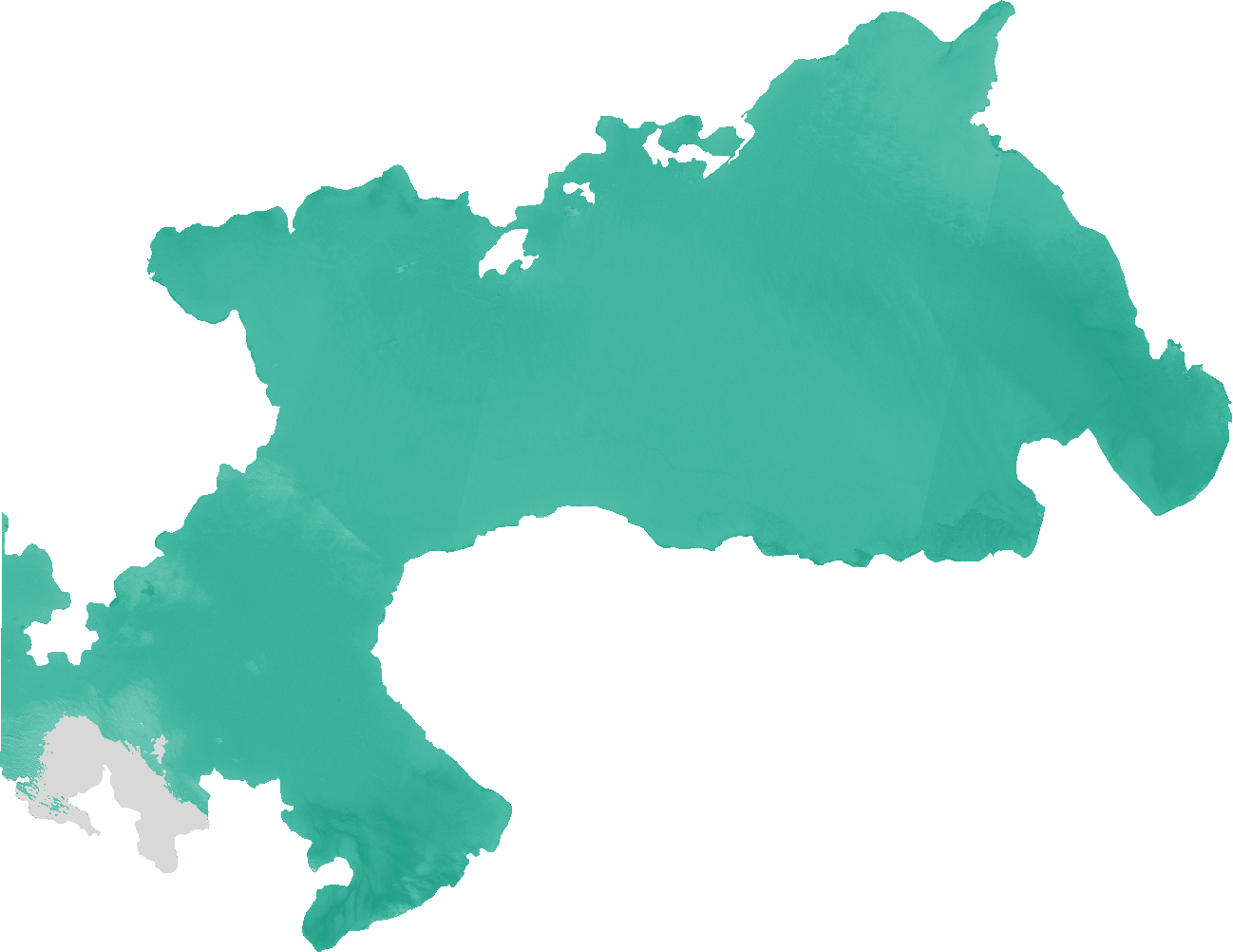
The Normalized Difference Water Index algorithm was developed by Gao (19964) being a measure of liquid water molecules in vegetation canopies that interacted with the incoming solar radiation. NDWI is sensitive to changes in liquid water content of vegetation canopies. It is less sensitive to atmospheric effects than NDVI. NDWI does not remove completely the background soil reflectance effects therefore it should be considered as an independent vegetation index. It is complementary to not a substitute for NDVI. The NDWI results from the following equation: NDWI = (IR_factor * near_IR - mir_factor * middle_IR) / (IR_factor * near_IR + mir_factor * middle_IR)

The Normalized Difference Pond Index algorithm was developed by J.P Lacaux et al. (2006).The NDPI makes it possible not only to distinguish small ponds and water bodies (down to 0.01 ha) but also to differentiate vegetation inside ponds from that in their surroundings The NDPI results from the following equation: NDPI = (mir_factor * middle_IR - green_factor * green) / (mir_factor * middle_IR + green_factor * green)

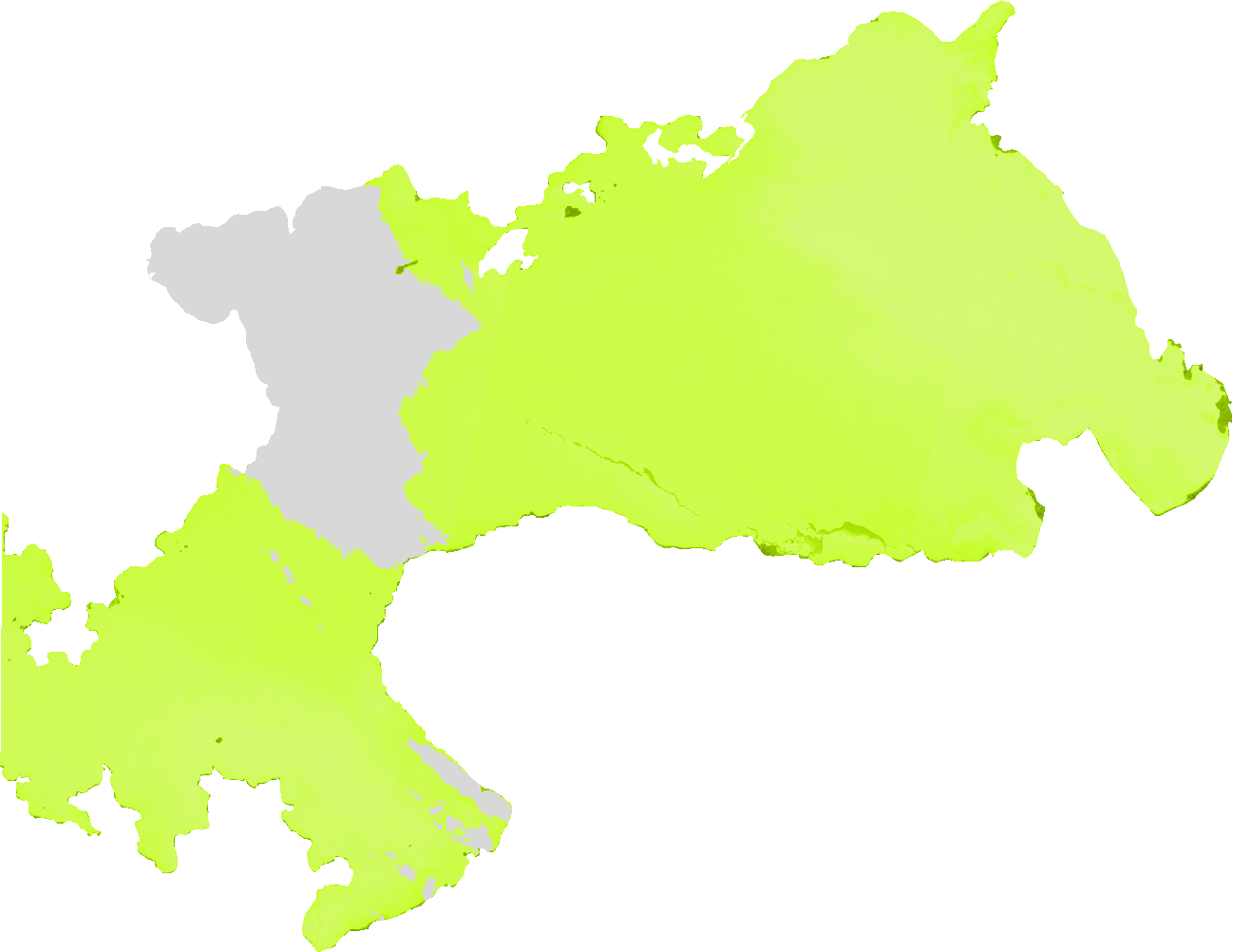
The Normalized Difference Pond Index algorithm was developed by J.P Lacaux et al. (2006).The NDPI makes it possible not only to distinguish small ponds and water bodies (down to 0.01 ha) but also to differentiate vegetation inside ponds from that in their surroundings The NDPI results from the following equation: NDPI = (mir_factor * middle_IR - green_factor * green) / (mir_factor * middle_IR + green_factor * green)

The Normalized Difference Pond Index algorithm was developed by J.P Lacaux et al. (2006).The NDPI makes it possible not only to distinguish small ponds and water bodies (down to 0.01 ha) but also to differentiate vegetation inside ponds from that in their surroundings The NDPI results from the following equation: NDPI = (mir_factor * middle_IR - green_factor * green) / (mir_factor * middle_IR + green_factor * green)

The Normalised Difference Turbidity Index (NDTI) quantifies the difference in reflectance between specific spectral bands which correlates with suspended sediment and turbidity levels.