The Normalised Difference Turbidity Index (NDTI) quantifies the difference in reflectance between specific spectral bands which correlates with suspended sediment and turbidity levels.

The Transformed Soil Adjusted Vegetation Index (TSAVI) method is a vegetation index that minimizes soil brightness influences by assuming the soil line has an arbitrary slope and intercept. TSAVI = (s *(NIR - s * Red - a)) / (a * NIR + Red - a * s + X * (1 + s2))

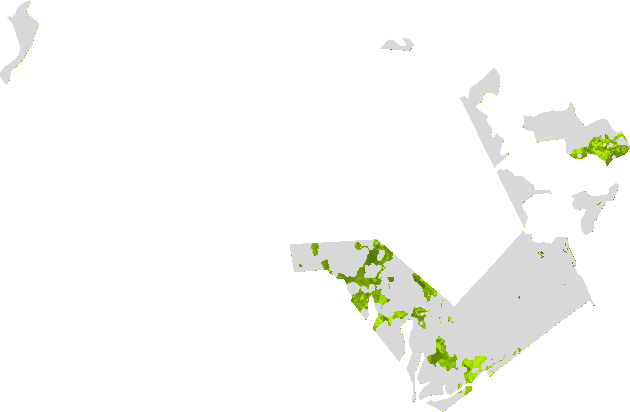
The Normalized Burn Ratio Index (NBR) uses the NIR and SWIR bands to emphasize burned areas while mitigating illumination and atmospheric effects. NBR = (NIR - SWIR) / (NIR+ SWIR)

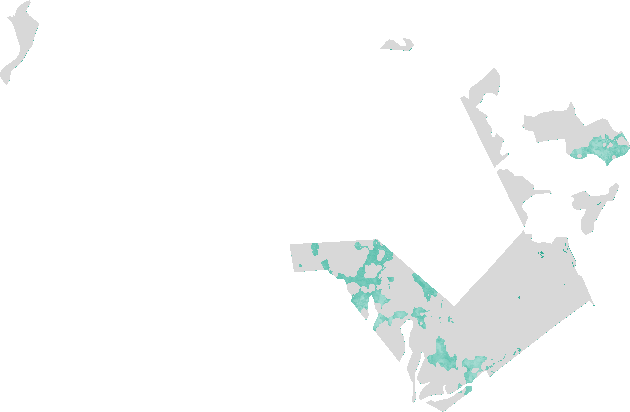
The Modified Normalized Difference Water Index algorithm was developed by Xu 2006 and can enhance open water features while efficiently suppressing and even removing built-up land noise as well as vegetation and soil noise. The greater enhancement of water in the MNDWI-image will result in more accurate extraction of open water features as the built-up land soil and vegetation all negative values and thus are notably suppressed and even removed. The MNDWI results from the following equation: MNDWI = (green_factor * green - mir_factor * middle_IR) / (green_factor * green + mir_factor * middle_IR)

MCARI gives a measure of the depth of chlorophyll absorption and is very sensitive to variations in chlorophyll concentrations as well as variations in Leaf Area Index (LAI). MCARI values are not affected by illumination conditions the background reflectance from soil and other non-photosynthetic materials observed.

The Normalized Difference Water Index algorithm was developed by Gao (19964) being a measure of liquid water molecules in vegetation canopies that interacted with the incoming solar radiation. NDWI is sensitive to changes in liquid water content of vegetation canopies. It is less sensitive to atmospheric effects than NDVI. NDWI does not remove completely the background soil reflectance effects therefore it should be considered as an independent vegetation index. It is complementary to not a substitute for NDVI. The NDWI results from the following equation: NDWI = (IR_factor * near_IR - mir_factor * middle_IR) / (IR_factor * near_IR + mir_factor * middle_IR)

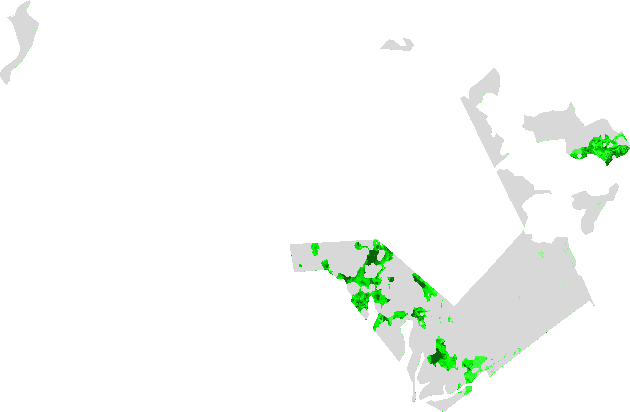
The Pigment Specific Simple Ratio (chlorophyll index) algorithm was developed by Blackburn (1998). It investigates the potential of a range of spectral approaches for quantifying pigments at the scale of the whole plant canopy. When applying existing narrow-band pigment indices the PSSR algorithms have the strongest and most linear relationships with canopy concentration per unit area of Chl a (Chlorophyll a) Chl b (Chlorophyll b) and Cars (carotenoids). The PSSRa results from the following equation: PSSRa = (IR_factor * near_IR) / (red_factor * red)

The Normalized Difference Pond Index algorithm was developed by J.P Lacaux et al. (2006).The NDPI makes it possible not only to distinguish small ponds and water bodies (down to 0.01 ha) but also to differentiate vegetation inside ponds from that in their surroundings The NDPI results from the following equation: NDPI = (mir_factor * middle_IR - green_factor * green) / (mir_factor * middle_IR + green_factor * green)

The Transformed Normalized Difference Vegetation Index algorithm indicates a relation between the amount of green biomass that is found in a pixel. (Senseman et.al. 1996). Transformed Normalised Difference Vegetation index (TNDVI) is the square root of the NDVI. It has higher coefficient of determination for the same variable and this is the difference between TNDVI and NDVI. The formula of TNDVI has always positive values and the variances of the ratio are proportional to mean values. The TNDVI results from the following equation: TNDVI = sqrt( (IR_factor * near_IR - red_factor * red) / (IR_factor * near_IR + red_factor * red) + 0.5)

LAI is defined as half the developed area of photosynthetically active elements of the vegetation per unit horizontal ground area. It determines the size of the interface for exchange of energy (including radiation) and mass between the canopy and the atmosphere. This is an intrinsic canopy primary variable that should not depend on observation conditions. LAI is strongly non linearly related to reflectance. Therefore its estimation from remote sensing observations will be strongly scale dependent (Garrigues et al. 2006a Weiss et al. 2000). Note that vegetation LAI as estimated from remote sensing will include all the green contributors i.e. including understory when existing under forests canopies.