Difference Vegetation Index: This index is sensitive to the amount of vegetation. The Difference Vegetation Index algorithm is sensitive to the amount of vegetation. This is the simplest vegetation index: - Sensitive to the amount of vegetation - Distinguishes between soil and vegetation - Does NOT deal with the difference between reflectance and radiance caused by the atmosphere or shadows. The DVI results from the following equation: DVI = (IR_factor * near_IR - red_factor * red). In the area of red the incoming solar radiation won't be extensively absorbed by the pigments of the mesophyll inside the folios primarily by the chlorophyll. In the area of the near infrared in contrast the bigger part of the incoming radiation was reflected.

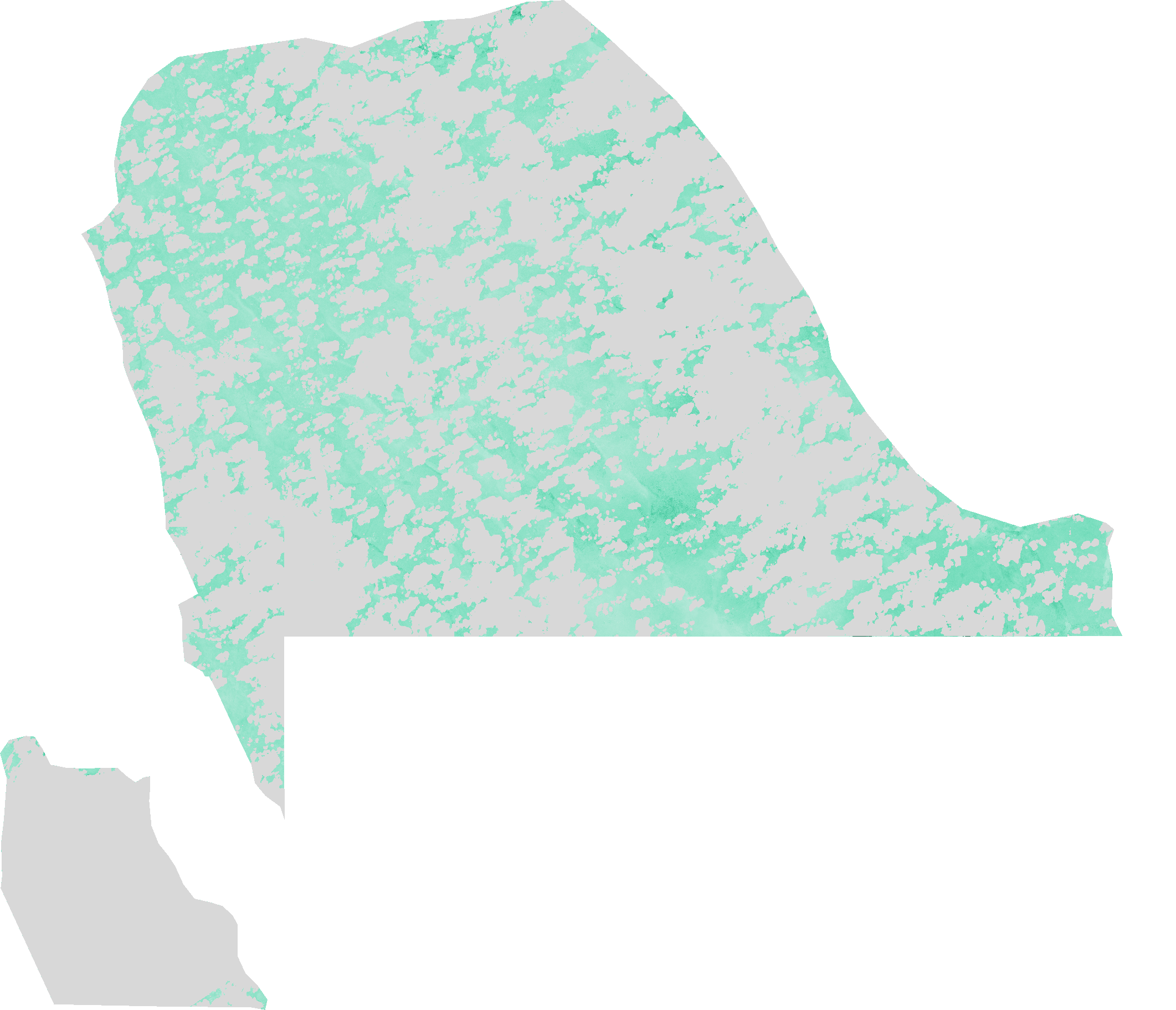
Canopy water content (CWC) the amount of water stored in the vegetation canopy is typically determined by multiplying the leaf water content by the canopy leaf area index (LAI). This calculation incorporates information about the leaf water condition and the canopy structure [1]. CWC is a critical parameter for assessing vegetation growth and monitoring drought stress. It is influenced by soil water supply and atmospheric demand.

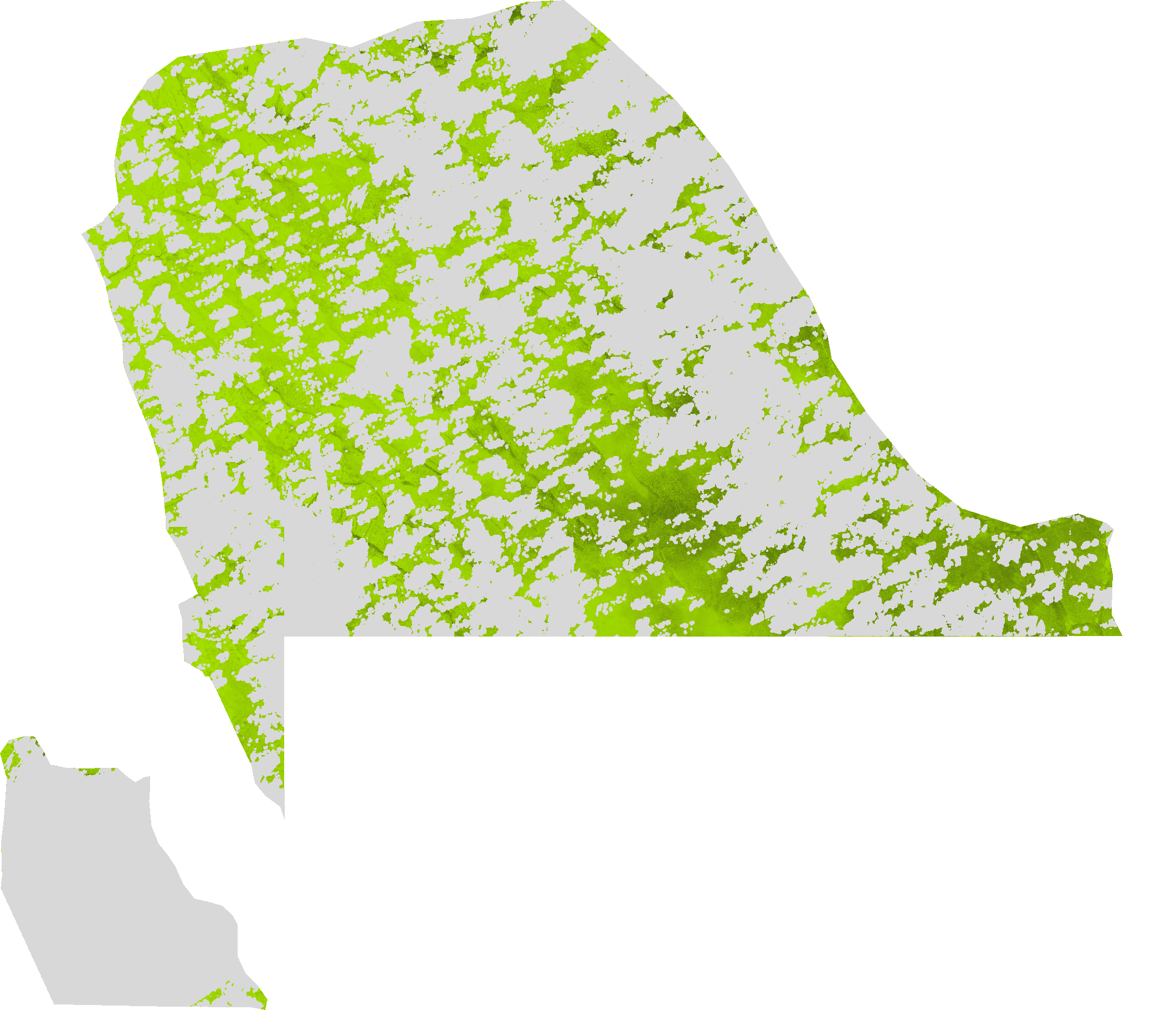
Cover fraction: FVC is used to separate vegetation and soil in energy balance processes including temperature and evapotranspiration. It is computed from the leaf area index and other canopy structural variables and does not depend on variables such as the geometry of illumination as compared to FAPAR

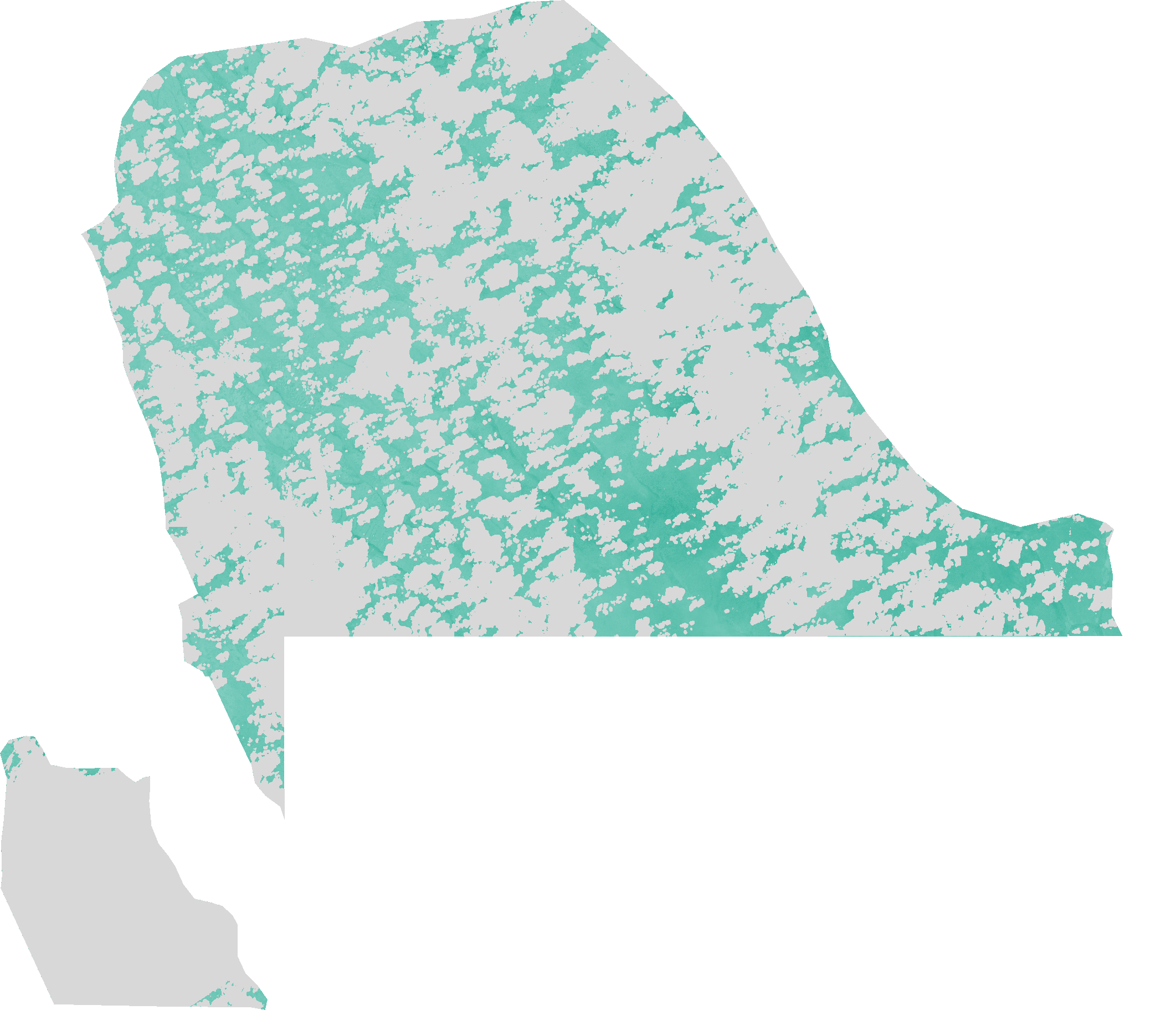
The Normalized Difference Water Index algorithm was developed by Gao (19964) being a measure of liquid water molecules in vegetation canopies that interacted with the incoming solar radiation. NDWI is sensitive to changes in liquid water content of vegetation canopies. It is less sensitive to atmospheric effects than NDVI. NDWI does not remove completely the background soil reflectance effects therefore it should be considered as an independent vegetation index. It is complementary to not a substitute for NDVI. The NDWI results from the following equation: NDWI = (IR_factor * near_IR - mir_factor * middle_IR) / (IR_factor * near_IR + mir_factor * middle_IR)

The Normalized Burn Ratio Index (NBR) uses the NIR and SWIR bands to emphasize burned areas while mitigating illumination and atmospheric effects. NBR = (NIR - SWIR) / (NIR+ SWIR)

The Transformed Normalized Difference Vegetation Index algorithm indicates a relation between the amount of green biomass that is found in a pixel. (Senseman et.al. 1996). Transformed Normalised Difference Vegetation index (TNDVI) is the square root of the NDVI. It has higher coefficient of determination for the same variable and this is the difference between TNDVI and NDVI. The formula of TNDVI has always positive values and the variances of the ratio are proportional to mean values. The TNDVI results from the following equation: TNDVI = sqrt( (IR_factor * near_IR - red_factor * red) / (IR_factor * near_IR + red_factor * red) + 0.5)

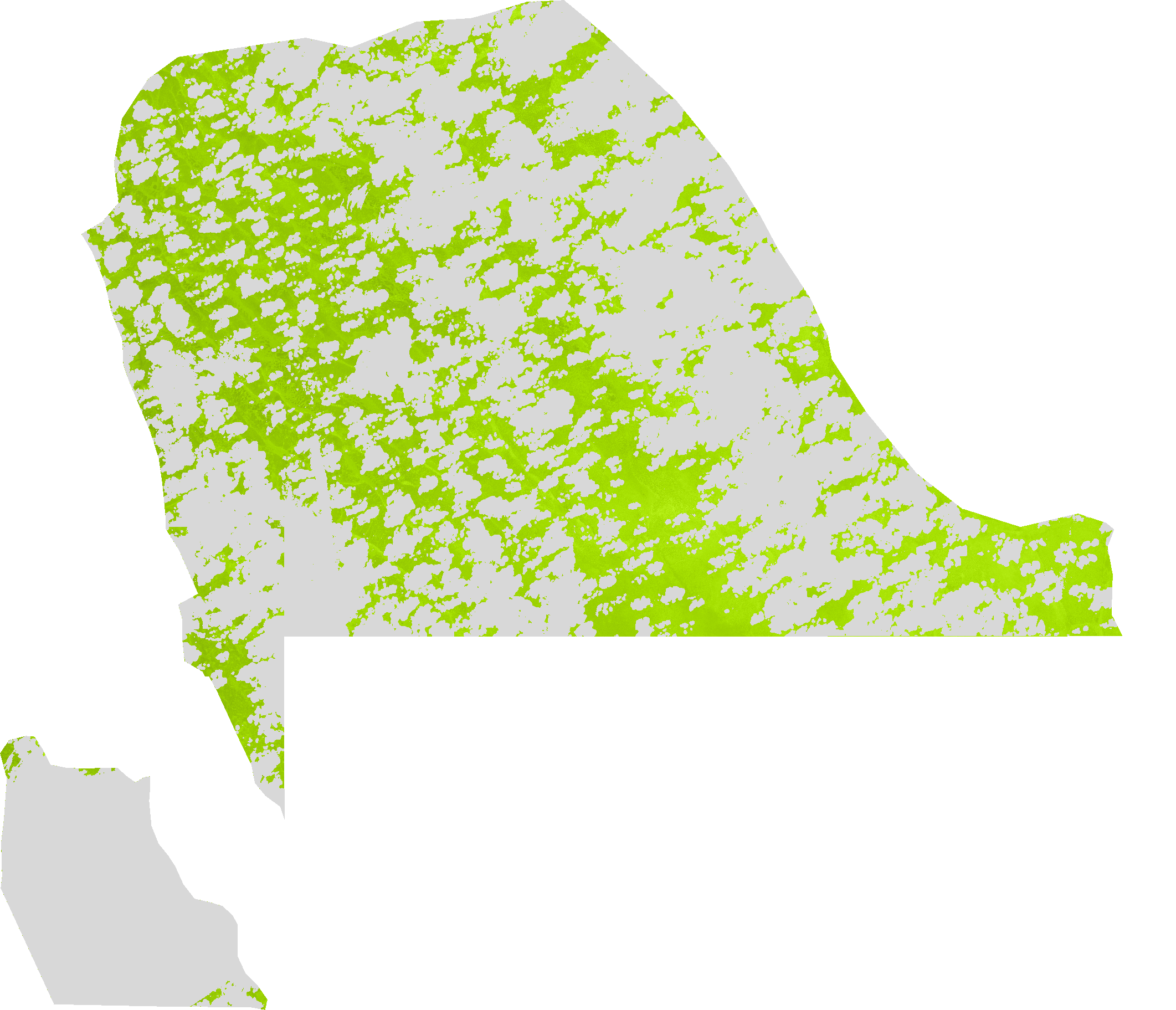
The Normalised Difference Turbidity Index (NDTI) quantifies the difference in reflectance between specific spectral bands which correlates with suspended sediment and turbidity levels.

MCARI gives a measure of the depth of chlorophyll absorption and is very sensitive to variations in chlorophyll concentrations as well as variations in Leaf Area Index (LAI). MCARI values are not affected by illumination conditions the background reflectance from soil and other non-photosynthetic materials observed.

The Modified Normalized Difference Water Index algorithm was developed by Xu 2006 and can enhance open water features while efficiently suppressing and even removing built-up land noise as well as vegetation and soil noise. The greater enhancement of water in the MNDWI-image will result in more accurate extraction of open water features as the built-up land soil and vegetation all negative values and thus are notably suppressed and even removed. The MNDWI results from the following equation: MNDWI = (green_factor * green - mir_factor * middle_IR) / (green_factor * green + mir_factor * middle_IR)

Inverted Red-Edge Chlorophyll Index: The Inverted Red-Edge Chlorophyll Index algorithm incorporates the reflectance in four bands to estimate canopy chlorophyll content (Guyot and Baret 1988 Clevers et al. 2000). The 'red edge' is the name given to the abrupt reflectance change in the 680-740 nm region of vegetation spectra that is caused by the combined effects of strong chlorophyll absorption and leaf internal scattering. Increases in the amount of chlorophyll visible to the sensor either through an increase in leaf chlorophyll content or Leaf Area Index (LAI) result in a broadening of a major chlorophyll absorption feature centred around 680 nm. The effect is to cause a movement of the point of maximum slope termed the red edge position (REP). The position of the red edge has been used as an indicator of stress and senescence of vegetation (Collins1978 Horler et al. 1983 Rock et al. 1988 Boochs et al. 1990 Jago and Curran 1995). The IRECI results from the following (Sensor-dependent) equation: IRECI = (IR_factor * near_IR - red1_factor * red1) / (red2_factor * red2 / red3_factor * red3). For Sentinel-2 the formula is: (B7 - B4) / (B5 / B6) where (Central wavelength/Bandwidth): B7 = 783 nm (15 nm) B6 = 740 nm (15 nm) B5 = 705 nm (15 nm) B4 = 665 nm (30 nm)